重力储能直流环节电池多模式控制方法｜《中国电力》

重力储能需要通过电力拖动系统实现机电能量转换，典型结构由外部局域电网、新能源发电装置、电力拖动装置、电池储能装置连接构成，系统结构如图1所示。

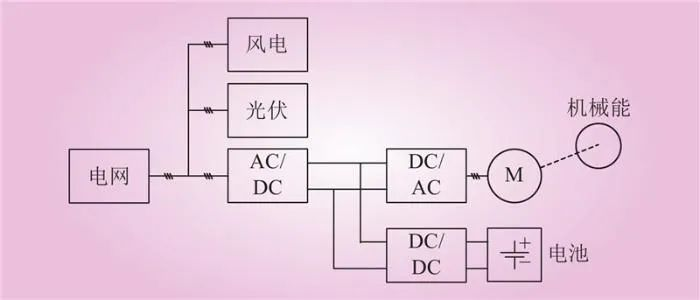
图1  重力储能系统一般结构

Fig.1  General structure of gravity energy storage system

重力储能机械储能的核心是四象限电力拖动系统。一般由AC/DC、直流电容、DC/AC（电机控制器）、电动机、机械传动机构、工作机构等构成。如果考虑到直流母线的电压，则在系统内布置电池和DC/DC变换器用来进一步优化系统性能。采用混合储能方式，有利于不同储能方式之间的配合从而获得更优化的整体性能。

1.2  运动学模型

电机通过传动装置拖动一个卷筒，通过卷绕卷筒上的钢丝绳升起或降落重物。对于电力拖动方式的储能系统，重物在卷筒上产生等效的总飞轮惯量，其运动方程为

式中：T为电磁转矩，N·m；TL为负载转矩，N·m；G为重物总重力，N；D为卷绕筒直径，m；n为转速，转/min。

重力储能具有位能性转矩负载特性，负载转矩是由重力作用产生。重力产生的TL的大小和作用方向与转速无关。无论是提升重物还是下放重物，重力的作用方向不变。如果以提升作为运动的正方向，即n为正值，TL是阻碍运动的阻转矩，为正值；当下放重物，即n为负值，TL的方向不变，仍为正，表明此时TL是促进转动的，由提升重物时的阻转矩变成了拖动转矩。其特性位于第Ⅰ和第Ⅳ象限内。考虑系统的摩擦转矩等叠加作用，系统的转矩特性如图2所示。

图2  电磁转矩与负载转矩的关系

Fig.2  Relationship between electromagnetic torque and load torque

由于重力提升或下降过程中，阻力方向与运动方向相反，因此负载转矩TL为

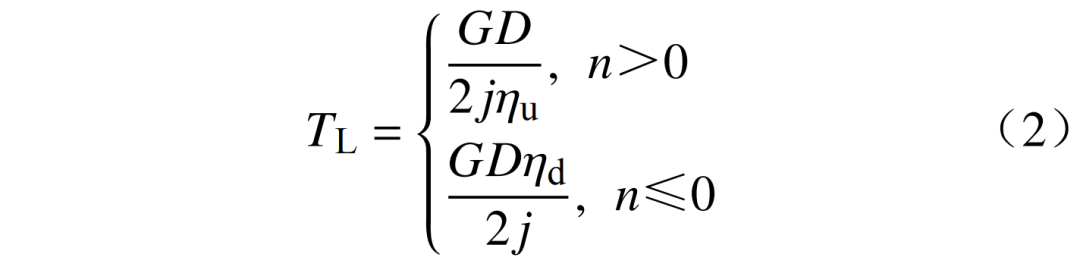
式中：j为传动机构传动比；ηu为提升效率，100%；ηd为下降效率，100%。

1.3  基本机电转化能量模型

对于不同种类的电机和控制方式，电机控制器基本方程具有较大的差异。受到机械摩擦、调速过程中的电机特性和传动方式等影响，很难建立统一的数学模型。但从功率角度，一般来说电机功率满足如下关系。

式中：P1为定子输入功率，W；Pcu为铜损功率，W；Pfe为铁损功率，W；Pe为电磁功率，W；Pμ 为摩擦引起的总功率，W；P2为转子输出功率，W。

在启动和调速过程中，变频器不但需要提供电机启动和调速过程中产生的重力势能，还要提供由于重物速度变化而产生的动能变量和在电机上产生的损耗。因此主要分为变速（启动、加速、减速）和匀速运行两个工况。在匀速工况，重物克服自身重力和摩擦力的阻碍，实现能量的存储和释放，其满足一般方程为

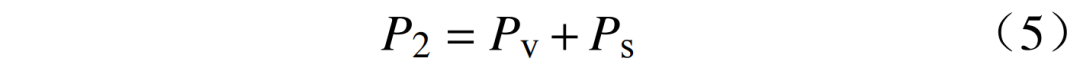
式中：Pv为重物及传动机构存储的动能功率，W；Ps为重物的势能存储功率，W。

1.4  能量储存模型

拖动系统在能量存储过程的分析条件为：1）为了突出动态条件下的机械能和电能交换的主要过程，电磁过渡过程的影响忽略不计，只考虑机械过渡过程对能量存储性能的影响。2）仅考虑能量的转换过程，忽略特定驱动形式的电磁特性，电源电压、磁通和负载转矩在过渡过程中保持恒定不变。3）由于重力储能的重物质量较大，因此忽略传动机械结构的转动惯量和重力影响。4）为提高系统的经济性，仅考虑电池容量远小于重物储能容量的情况。为了突出重力储能与电池储能的配合情况与应用效果，本文仅研究输入功率大于电池容量的情况。

设重物的提升高度为h，重物的质量为m，重物的速度为v，则储能装置的稳态下的机械功率Ps、储存重力势能能量Ws和运动系统的总动能Wv分别为

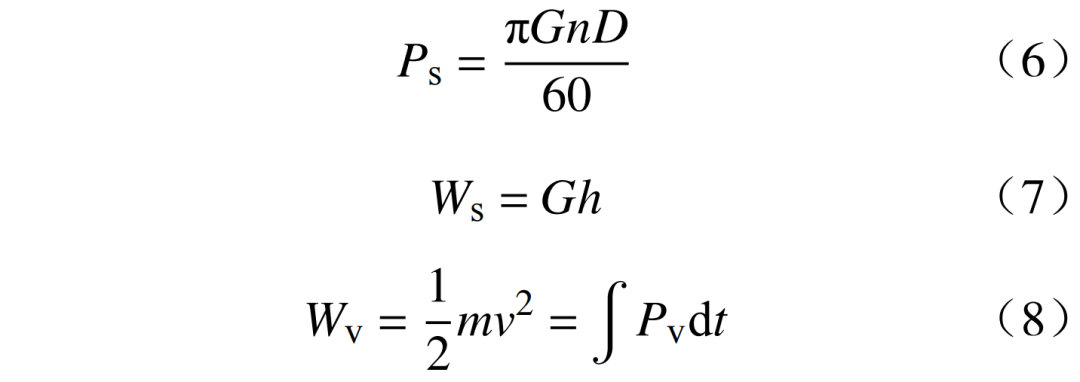
在储能装置内部通过直流母线将电池储能装置和电机逆变器连接。在存储能量时，逆变器驱动电动机工作，从直流母线获取能量提升重物滑车，重力势能和动能同时增加。但是需要注意的是机械功率是速度的函数，重力储能的储存功率与转速n成正比。由于重力储能的机械惯性较大，其存储能力提升需要经历较长的重物加速过程，相对于电池储能方式，重力储能具有较突出的功率滞后特性。

1.5  电池及DC/DC变换器模型

重力储能系统中机械时间常数和系统效率与电池系统相差较大，出于化简系统分析模型的角度和对直流母线稳定特性分析的目的，建立基于能量角度的简化电池及DC/DC变换器模型为

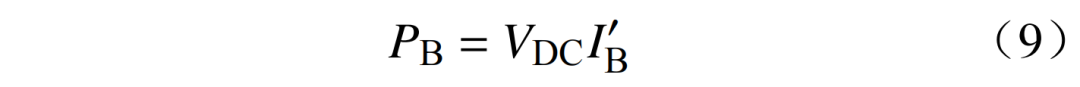
式中：PB为电池输入的功率，W；为电池输入电流，A；VDC为直流母线电压，V。

同样基于时间常数特征的考虑，设置电池电量采用安时法简化模型为

式中：SOC为电池的荷电状态，100%；SOC0为电池的初始荷电状态，100%；IB为电池的等效电流，A；Qmax为电池的总电量，C。

02

2.1  储能设计目标

储能设计目标为：1）最大限度地利用可再生能源目标。2）快速稳定系统内的能量平衡。3）提高储能效率和品质。

上述目标函数为

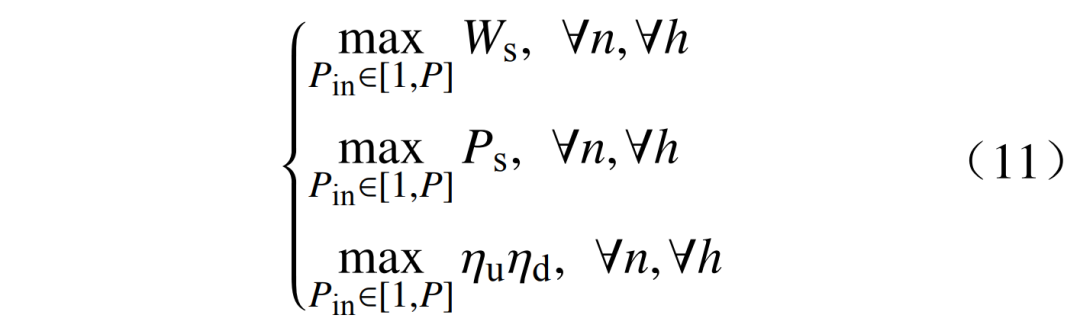
式中：Pin为系统输入功率；P为系统容量。

2.2  系统约束条件

1）母线电压约束为

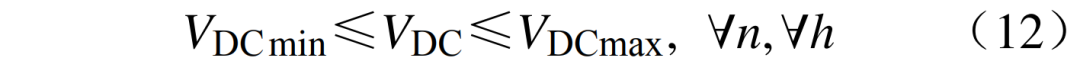
式中：VDCmax、VDCmin分别为直流母线的电压上下限。

母线电压维持稳定的条件为

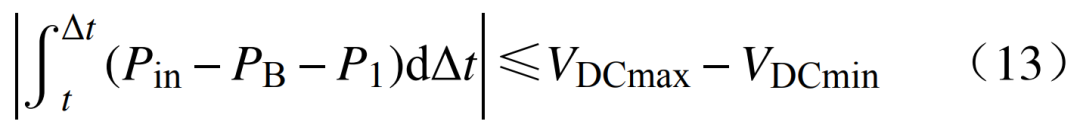
式中：Δt为时间间隔。

2）电池荷电状态约束为

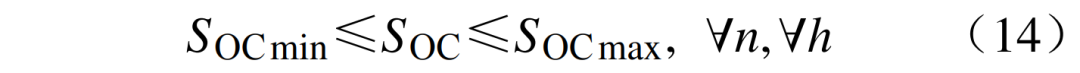
式中：SOCmax、SOCmin分别为荷电状态上下限。

3）变频器功率约束为

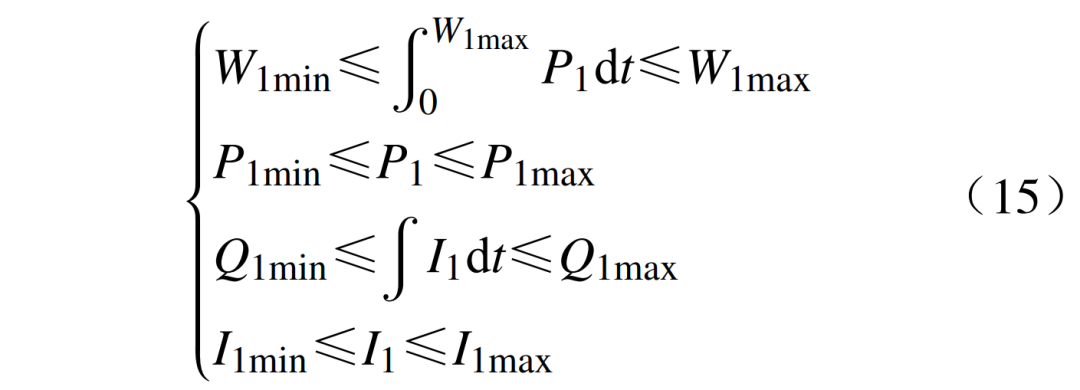
式中：W1max、W1min为变频器的输入能量上下限；P1max、P1min为变频器输入功率上下限；Q1max、Q1min为变频器输入电量上下限；I1max、I1min为变频器输入电流上下限。

4）重物加速度约束为

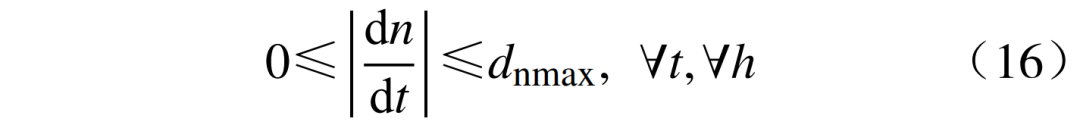
式中：dnmax为重物的最大加速度。

03

储能单元中接收（释放）的功率与变频器吸收（释放）的功率不平衡时，直流母线电压将发生波动。分级运行控制能够获得较好的系统功率分配，但是由于重力储能系统中重力储能和电池系统的差异较大，功率波动对直流总线电平的影响比较剧烈，需要提出相应控制方法对母线电压进行协调控制。

3.1  重力储能运行模型

建立基于能量角度的重力储能仿真模型，整体结构如图3所示，主要包括变频器的AC/DC部分、DC/AC部分、直流母线的滤波电容、电池DC/DC和电池。物理量包括电容值C、母线电压VDC、电池荷电状态SOC、系统输入功率Pin、直流滤波电容吸收功率PDC、电池输入功率PB。

图3  仿真模型

Fig.3  System simulation model

3.2  模式划分及控制框图

构建控制模式如图4所示，将SOC和直流电压作为控制功率流的依据。

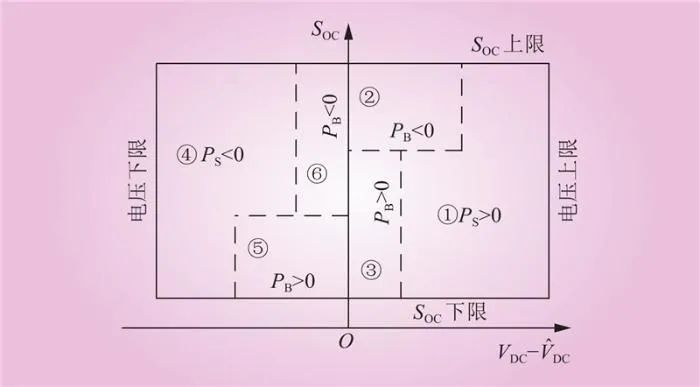
图4  控制模式图

Fig.4  Control model diagram

控制模式将直流母线电压实际值VDC与给定电压值之差作为横坐标，电池SOC值作为纵坐标。其有效空间为上下限包围的区域，并根据电池与重力储能工作特性的区别，将该区域分割为6个部分，分别对应不同的电池工作状态。

为简化系统结构，突出能量流关系，根据图4所示控制模式和式（3）~（5），对变频器控制模型参数进行归一化，并构建基于电机转矩控制模型，如图5所示。与VDC之差作为PI控制器（ksp、ksi分别为比例和积分常数）的输入变量。输出量与转矩常数kT相乘后获得电机的输出转矩T，经最大转矩约束限制后输出重物转矩TL。

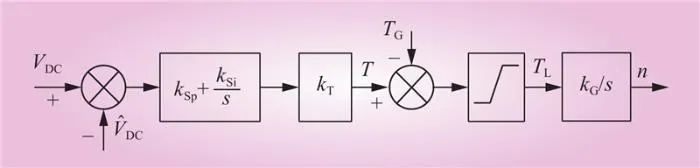
图5  变频器控制策略模型

Fig.5  Inverter control strategy model

构建电池控制策略如图6所示。其输入部分与图5所示控制策略模型一致，在PI控制模式上加入功率约束。将SOC和直流电压作为控制功率流的依据，输出量为电池的功率PB。输出功率在SOC限值保护、功率限制的基础上，将SOC限制式（14）和SOC的划分SOCLev引入控制策略构成前馈，形成模式控制框图如图7所示。

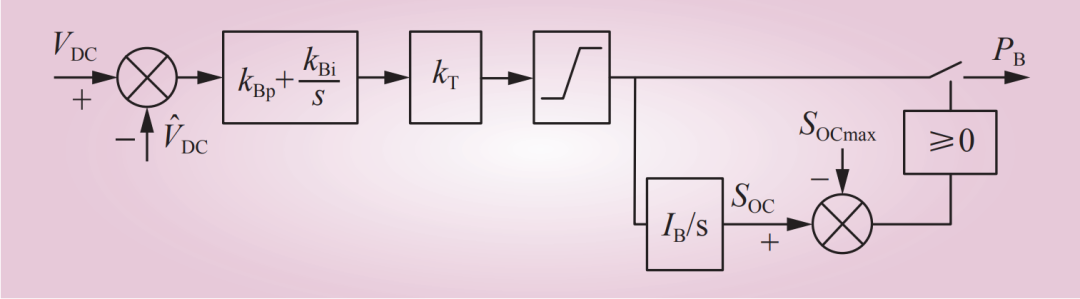
图6  电池控制策略

Fig.6  Battery control strategy

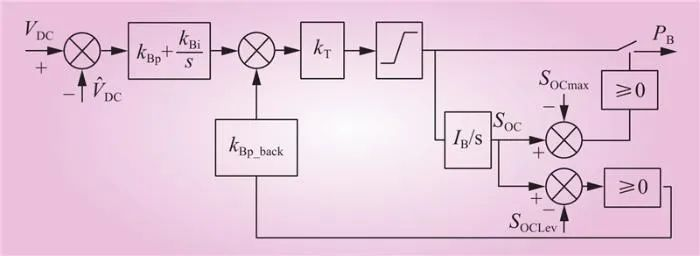
图7  模式控制框图

Fig.7  Mode control block diagram

3.3  仿真分析

3.3.1  案例1：突加输入功率情况下的系统特征

通过Matlab/Simulink进行时域仿真，并对算例的单位进行归一化处理，参数如表1所示。表1中：Pinnom为输入额定功率；VDCnom为直流母线额定电压；Tmax为电机最大输出转矩。

表1  系统参数

Table 1  System parameters

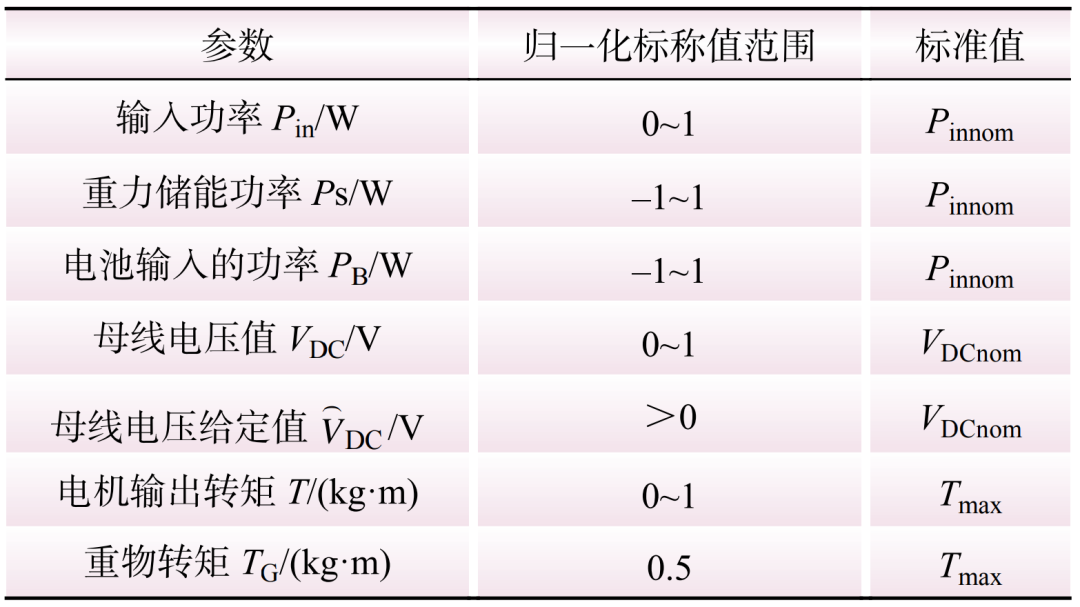
根据设计目标1），Pin为正（0~1）表示功率输入。PB和Ps可为功率双向流动（–1~1），设定重物储能的功率范围和电池储能的范围与输入功率的范围相同（–1~1），能够实现一种类型储能方式进行功率平衡。输入功率、电池功率和电机功率如图8所示。

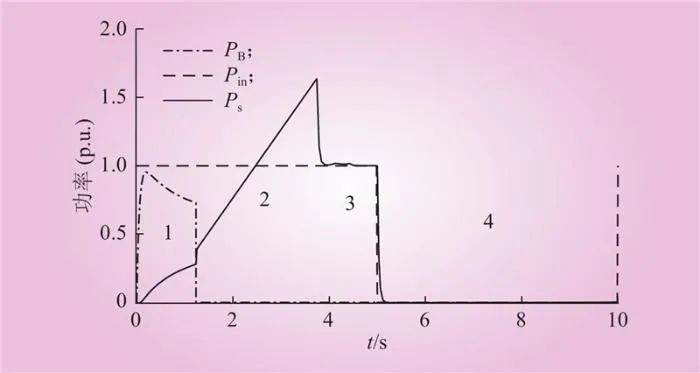
图8  输入功率、电池功率和电机功率（案例1）

Fig.8  Input power, battery power, and motor power (case 1)

作为对比，首先分析没有加入模式控制方式的系统特征。在没有考虑电池容量控制的情况下，当达到输入最大功率Pin的初始阶段，电池和电机同时分担输入功率。由于电池的响应更快，分担了较大的功率。但在一段时间后，电池储能能力逐渐饱和进而退出工作，输入功率完全由电机吸收。电机首先提高运行功率达到最大输出转矩，并在最大转矩条件下持续提高转速。

图9为转矩和转速响应的变化曲线。可以看到，在第1阶段，电池和电机分别吸收功率，由于电池的功率响应速度快于电机，此时主要由电池承担输入功率。但由于电池的容量限制，当达到SOC=1时，电池即退出吸收功率，此刻第1阶段也结束。此时负载转矩发生突变以响应直流环节的功率需求。需要注意的是经过阶段1的持续吸收电能，电机转速n已经逐渐提升。此时电机吸收功率的能力增加，可见通过电池储能的缓冲作用使得重力储能系统保持较平均的功率吸收能力，表明直流环节的电池储能的必要性。

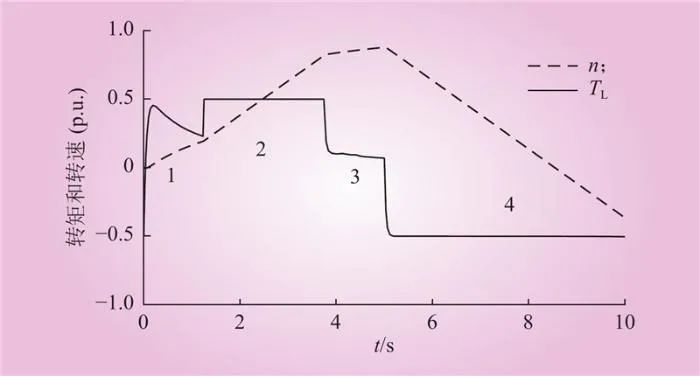
图9  转矩和转速变化曲线（案例1）

Fig.9  Torque and speed curve (case 1)

通过图9可见，在第2阶段的转矩达到最大值（本例中设定电磁转矩为归一化标准，TG/Tmax=0.5）。表明该阶段系统储能能力达到最大极限，直接导致如图10系统直流电压的超限。

图10  直流母线电压值（案例1）

Fig.10  DC bus voltage (case 1)

电压超限值与电池容量和电机容量相关。增加电池容量和增加电机的容量能够减少系统直流母线电压的升高，但过大的电池容量会造成系统成本上升。而提高电机容量有利于提高暂态功率的响应能力，但需要根据输入容量范围、电机驱动系统的短时抗过载能力等方面综合权衡。

在第3阶段，重力储能功率恢复与输入功率相同。第4阶段，输入功率为零，电机转矩为零，重物在重力作用下恒定减速，动能转化为机械能。

3.3.2  案例2：输入功率频繁波动情况

由多个功率方波进行模拟新能源输入功率波动情况，如图11所示。输入功率周期为3 s，占空比为50%。第1个周期内，电池储能与图8类似。但在第2个周期内，由于电池已经充满，难以继续吸收功率造成直流母线电压产生较大的泵升（标幺值达到1.8）。在第3个周期后，由于电机的转速提升（如图12所示），重力储能的功率吸收能力提高，直流母线的电压的波动范围缩小，如图13所示。

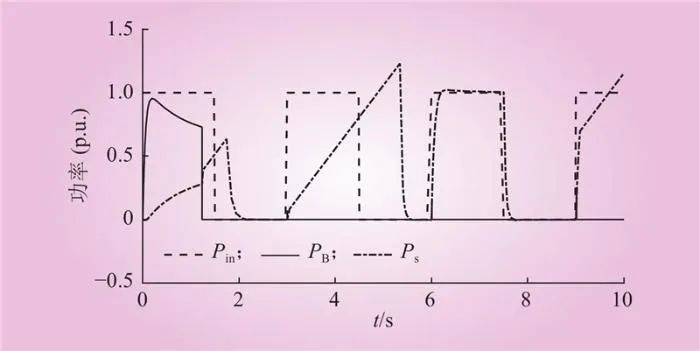
图11  输入功率、电池功率和电机功率（案例2）

Fig.11  Input power, battery power, and motor power (case 2)

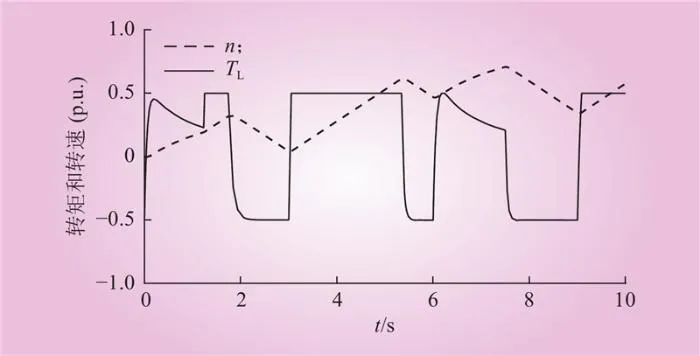
图12  转矩和转速变化曲线（案例2）

Fig.12  Torque and speed curve (case 2)

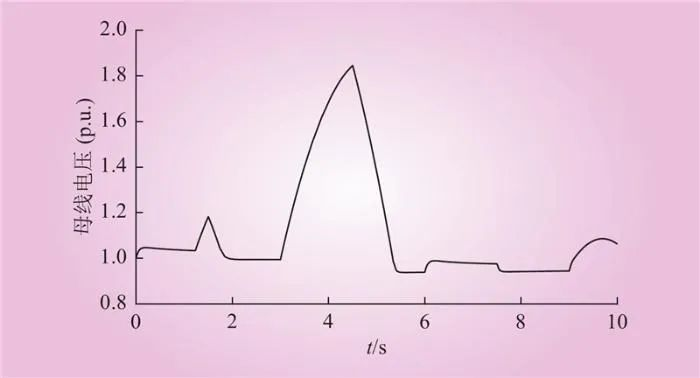
图13  直流母线电压值（案例2）

Fig.13  DC bus voltage (case 2)

3.3.3  案例3：模式划分控制情况

前面2种案例表明，在输入功率频繁波动情况下，由于电池的SOC饱和后退出工作，难以发挥电池快速响应的优势。因此，加入本文提出的模式划分控制模式，3.3.2中的相同输入功率波形的情况下，电池与重力储能发生功率交换（如图14所示）。首先降低了电池储能的SOC值，提高了储能系统的瞬时响应能力；其次将电池中储存的能量转移至重力储能，提高了重物的瞬时运行速度，进而提高了重力储能系统的瞬时储能功率。相对于图12，图15中的工作在最大转矩时间大幅度减少，对应图16中的直流母线电压的超调时间也大幅度减少，对于减少电机系统的损耗比较有利。通过分析可以看出，本文方法的本质是通过电池与重力储能的配合，利用了重力储能的能量远大于电池储能容量的特点，合理分配电池和重力储能间的储能容量和荷电状态，使得组合后的重力储能系统获得更加优化的综合性能。

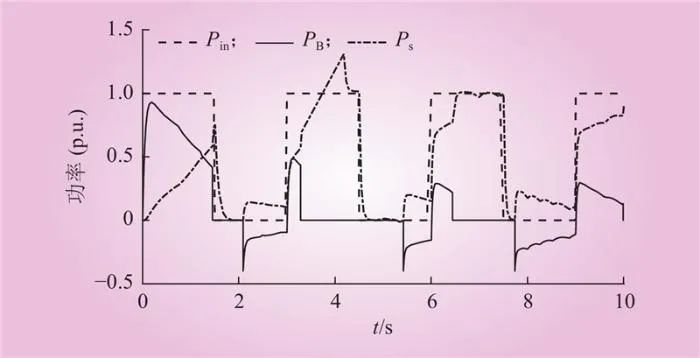
图14  输入功率、电池功率和电机功率（案例3）

Fig.14  Input power, battery power, and motor power (case 3)

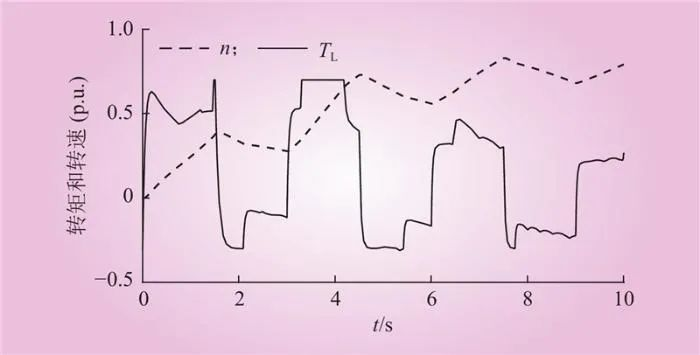
图15  转矩和转速变化曲线（案例3）

Fig.15  Torque and speed curve (case 3)

图16  直流母线电压值（案例3）

Fig.16  DC bus voltage (case 3)

04

本文根据重力储能的典型工作拓扑，构建了重力储能系统的典型工作模型和约束条件。仿真分析结果得出，重力储能直流环节的电池多模式控制方法能够较好适应重力储能方式的储能和滞后特性。能够在输入连续波动情况下合理调整电池的储能状态，较好地适配了电池快速响应特性和重力储能运行特性，改善单纯重力储能系统在响应特性方面的不足。通过电池能量方向的控制，可有效减少直流母线的电压波动峰值，对于稳定重力储能系统的内部稳定、提高重力储能系统的快速响应能力具有较大的意义。